1. 何谓单调栈

单调栈即满足单调性的栈结构。在遇到实际情况时，需要将不需要维护的数据从栈顶弹出，维护队列单调性。

一般的处理代码如下

// 单调递增栈，插入 t
while(!stk.empty() && stk.top() >= t) stk.pop();
stk.push(t);

2. 实际中的问题

P1 单调栈

给定一个长度为 N 的整数数列，输出每个数左边第一个比它小的数，如果不存在则输出 −1。

// 根据题意，对于某个待插入的数 t 来说，之前所有比 t 大的数， 对于 t 及以后的数来说都是无用的
// 1. Why 对 t 无用? 答： t 要找比 t 小的
// 2. Why 对 t 以后的数？答：如果往前找，找t就好了，比 t 前面且比 t 大的数不需要再比较了
#include <iostream>
#include <stack>

using namespace std;

int main() {
    int n, t;
    cin >> n;
    stack<int> stk;
    for (int i = 0; i < n; i++) {
        scanf("%d", &t);
        while (!stk.empty() && stk.top() >= t) stk.pop();
        if (stk.empty()) cout << "-1 ";
        else cout << stk.top() << " ";
        stk.push(t);
    }
    return 0;
}

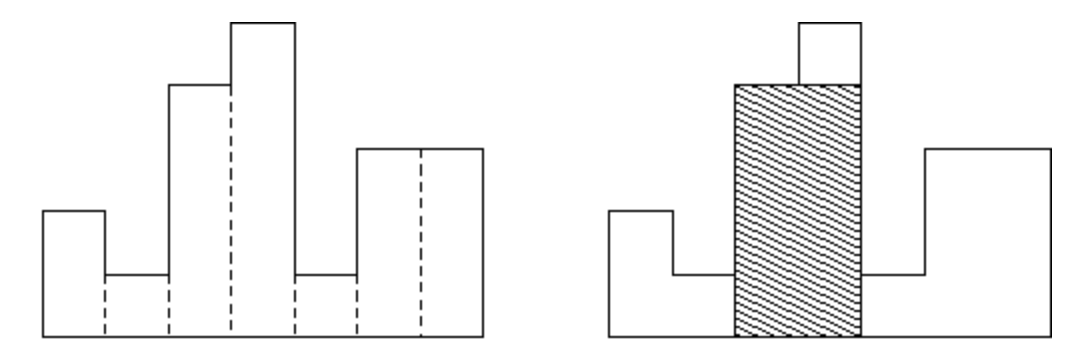
P2 直方图中最大的矩形

如下图所示，直方图是由在公共基线处对齐的一系列矩形组成的多边形。

矩形具有相等的宽度，但可以具有不同的高度。

例如，图例左侧显示了由高度为 2,1,4,5,1,3,32,1,4,5,1,3,3 的矩形组成的直方图，矩形的宽度都为 11：

现在，请你计算在公共基线处对齐的直方图中最大矩形的面积。

#include <iostream>
#include <cstring>
#include <algorithm>
#include <stack>

using namespace std;

typedef long long LL;

const int N = 1e5 + 10;

int l[N], r[N], g[N], n;

int main() {
    while (scanf("%d", &n), n) {
        for (int i = 1; i <= n; i++) scanf("%d", g + i);
        g[0] = -1, g[n + 1] = -1;
        // 初始化数组 l[i], 表示所有下标 i 左边第一个比他小的下标
        stack<int> stk;
        stk.push(0);
        for (int i = 1; i <= n; i++) {
            while (!stk.empty() && g[stk.top()] >= g[i]) stk.pop();
            l[i] = stk.top();
            stk.push(i);
        }
        while (!stk.empty()) stk.pop();
        stk.push(n + 1);
        // 初始化数组 r[i], 表示所有下标 i 右边第一个比他小的下标
        for (int i = n; i >= 1; i--) {
            while (!stk.empty() && g[stk.top()] >= g[i]) stk.pop();
            r[i] = stk.top();
            stk.push(i);
        }
        // 枚举所有以 i 为顶边的情况
        LL ans = 0;
        for (int i = 1; i <= n; i++) {
            ans = max(ans, (LL) g[i] * (r[i] - l[i] - 1));
        }
        cout << ans << endl;
    }
    return 0;
}

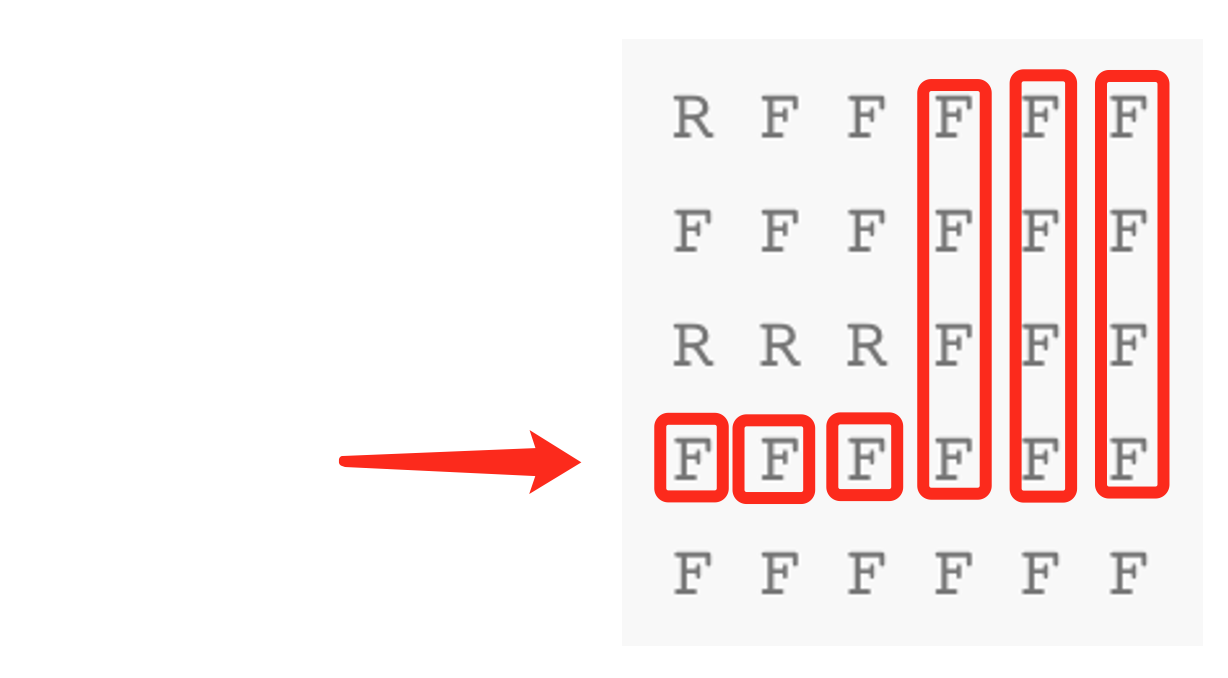
P3 城市游戏

求被 F 覆盖的最大矩形面积， 本题就是上一题直接的变形，枚举每一行，就可以看做是一个直方图

R F F F F F
F F F F F F
R R R F F F
F F F F F F
F F F F F F

#include <iostream>
#include <cstring>
#include <algorithm>
#include <stack>

using namespace std;

typedef long long LL;

const int N = 1010;

// mp[i][j] 表示第i行第j列方格上方包括自己有多少个F, 相当于上题中的矩形高度！！！
int l[N], r[N], mp[N][N];
int n, m;

int solve(int g[]) {
    g[0] = -1, g[n + 1] = -1;
    // 初始化数组 l[i], 表示所有下标 i 左边第一个比他小的下标
    stack<int> stk;
    stk.push(0);
    for (int i = 1; i <= n; i++) {
        while (!stk.empty() && g[stk.top()] >= g[i]) stk.pop();
        l[i] = stk.top();
        stk.push(i);
    }
    while (!stk.empty()) stk.pop();
    stk.push(n + 1);
    // 初始化数组 r[i], 表示所有下标 i 右边第一个比他小的下标
    for (int i = n; i >= 1; i--) {
        while (!stk.empty() && g[stk.top()] >= g[i]) stk.pop();
        r[i] = stk.top();
        stk.push(i);
    }
    // 枚举所有以 i 为顶边的情况
    LL ans = 0;
    for (int i = 1; i <= n; i++) {
        ans = max(ans, (LL) g[i] * (r[i] - l[i] - 1));
    }
    return ans;
}

int main() {
    cin >> m >> n;
    char c[3];
    int ans = 0;
    for(int i=1;i<=m;i++) {
        for(int j=1;j<=n;j++) {
            scanf("%s", &c);
            if(c[0] == 'F') mp[i][j] = mp[i-1][j] + 1;
        }
        ans = max(ans, solve(mp[i]));
    }
    cout << ans * 3 << endl;
    return 0;
}