1. 树状数组基本介绍与实现

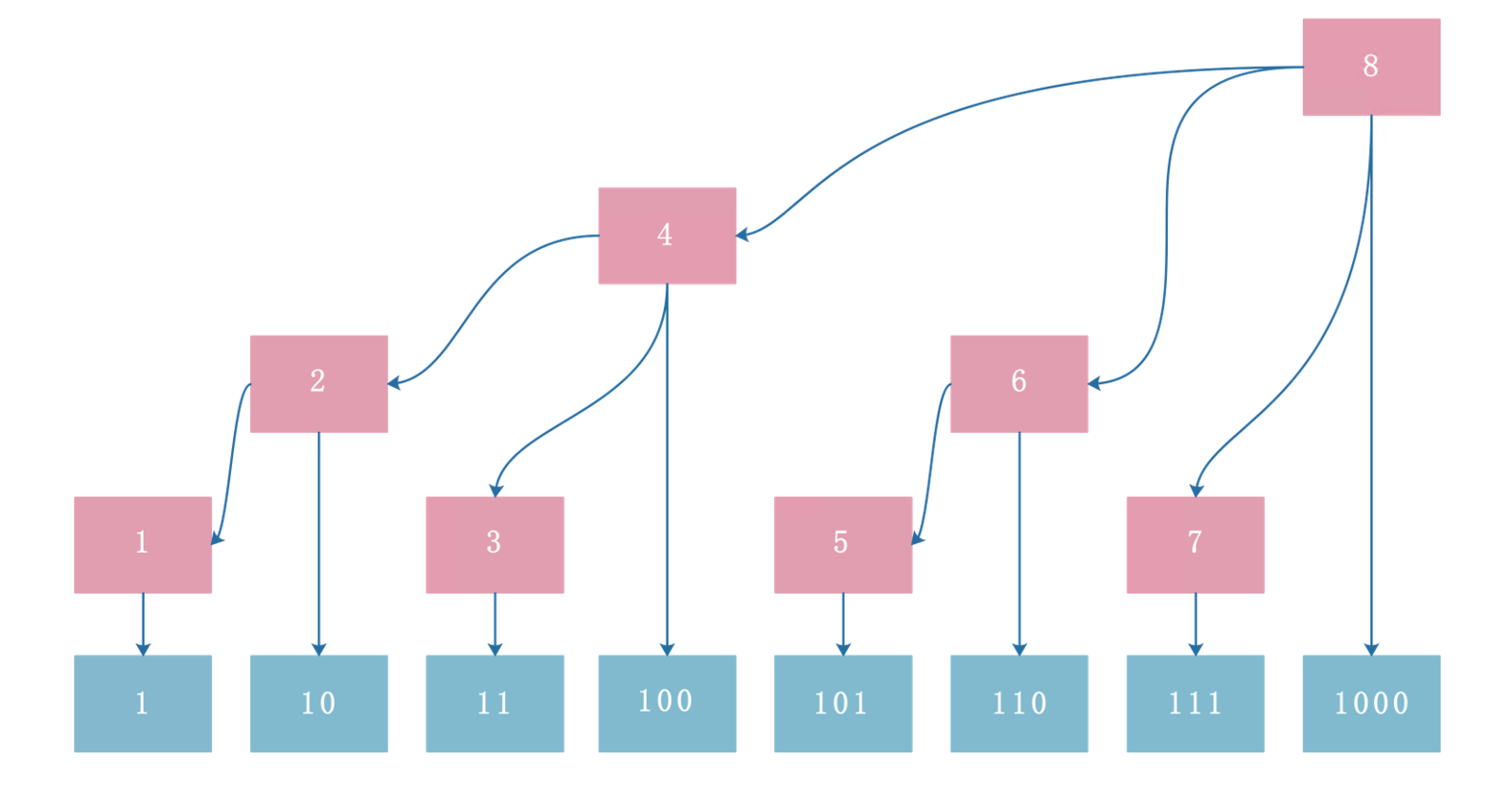
树状数组是一个动态维护前缀和的数据结构，其利用的是二进制位转化的关系，保证查询和插入的时间复杂度都是O (logN)， 空间复杂度为 O(N)。如下图所示，粉色代表开辟出的空间数组，代表指向的所有块的和。

如果要算出前7（111B）的和，如图可知，只需算出 4(100B)、6(110B)、7(111B) 3处的和即可，根据 7（111B）， 删去其2进制的末尾1即得到 6（110B）, 根据 6（110B）， 删去其2进制的末尾1即得到 4（100B）,使得其具有天然的关系性。（111 -> 110 -> 100）

lowbit数组：对于数 x ， 可得到其末尾 1 的值

int lowbit(int x) { return x & (-x); }

证明如下图

下面是实现方式（往往与离散化一起使用）

int bit[N];

int lowbit(int x) { return x & (-x); }

int query(int x) {
    int ans = 0;
    while (x > 0) {
        ans += bit[x];
        x -= lowbit(x);
    }
    return ans;
}

void add(int x, int val) {
    while (x < N) {
        bit[x] += val;
        x += lowbit(x);
    }
}

2. 一些基本使用

【例题】逆序对

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。

示例 1:

输入: [7,5,6,4]
输出: 5

实现代码如下

#include <vector>
#include <unordered_map>

using namespace std;

const int SIZE = 5e5 + 10;

class Solution {

    int bit[SIZE];

    int lowbit(int x) { return x & (-x); }

    int query(int x) {
        int ans = 0;
        while (x > 0) {
            ans += bit[x];
            x -= lowbit(x);
        }
        return ans;
    }

    void add(int x, int val) {
        while (x < SIZE) {
            bit[x] += val;
            x += lowbit(x);
        }
    }

    unordered_map<int, int> real2idx;

public:
    int reversePairs(vector<int> &nums) {
        vector<int> copyNum(nums);
        // 离散化
        sort(copyNum.begin(), copyNum.end());
        int cnt = 1;
        for (int num : copyNum) {
            if (real2idx.count(num)) continue;
            real2idx[num] = cnt++;
        }

        int ans = 0;
        for (int num : nums) {
            ans += query(SIZE - 1) - query(real2idx[num]);
            add(real2idx[num], 1);
        }
        return ans;
    }
};