【数据结构】Trie树
1. Trie 树基本介绍与实现
Trie(字典树)是一种用于实现字符串(不一定是字符串,如一个整数的二进制串等)快速检索的多叉树结构。如下图所示,是字符串 "cab"、"cos"、"car"、"cat"、"cate"、"rain" 插入操作。
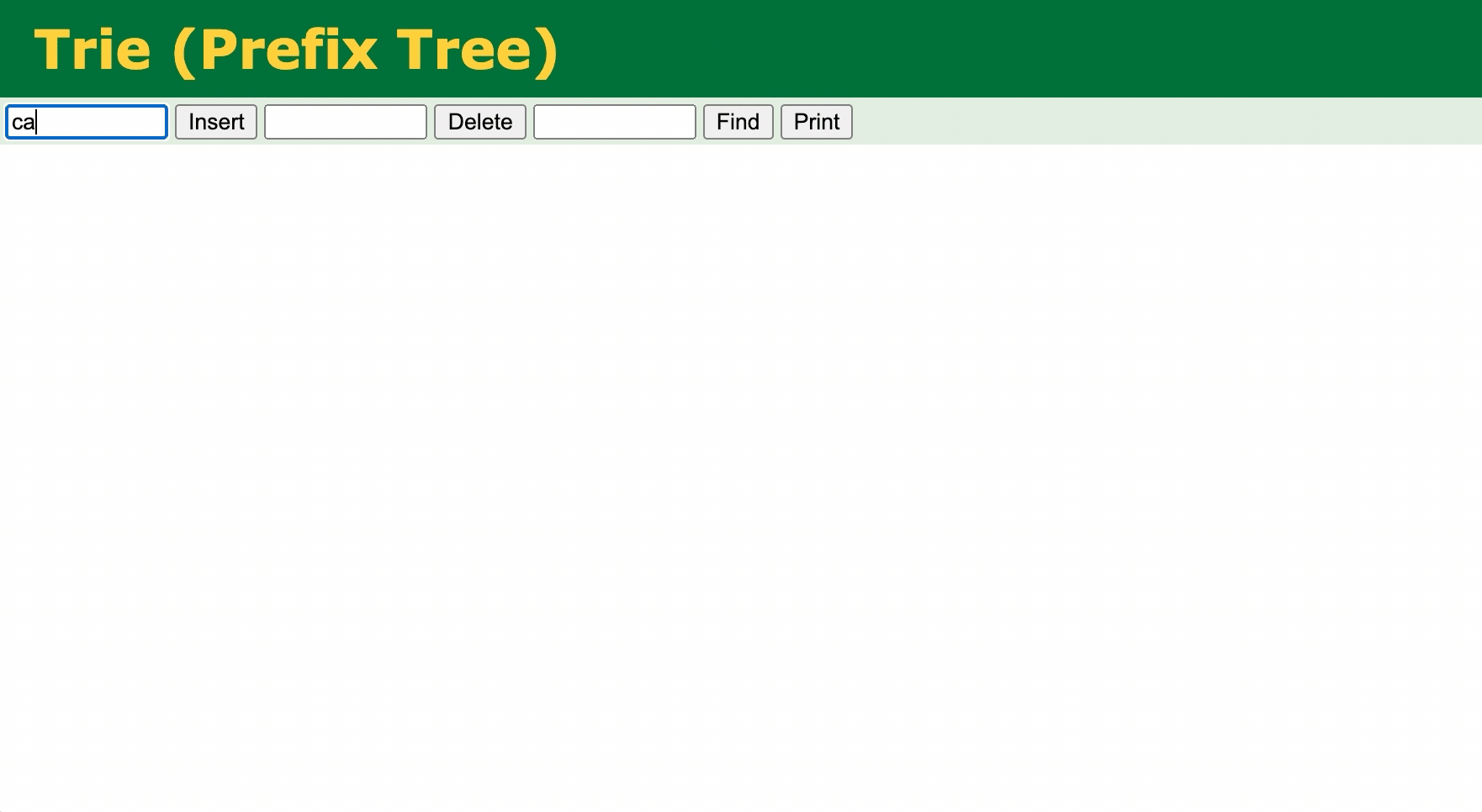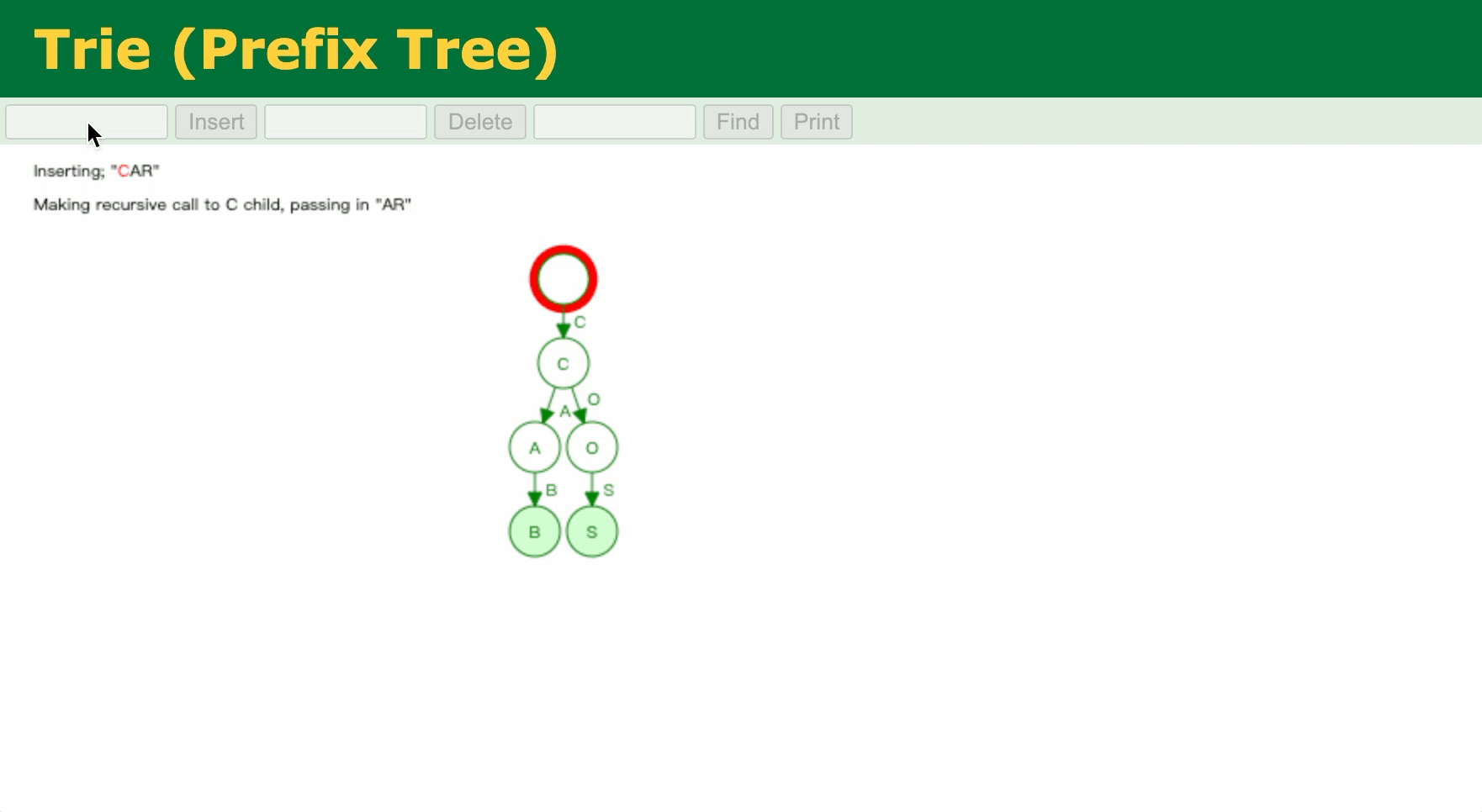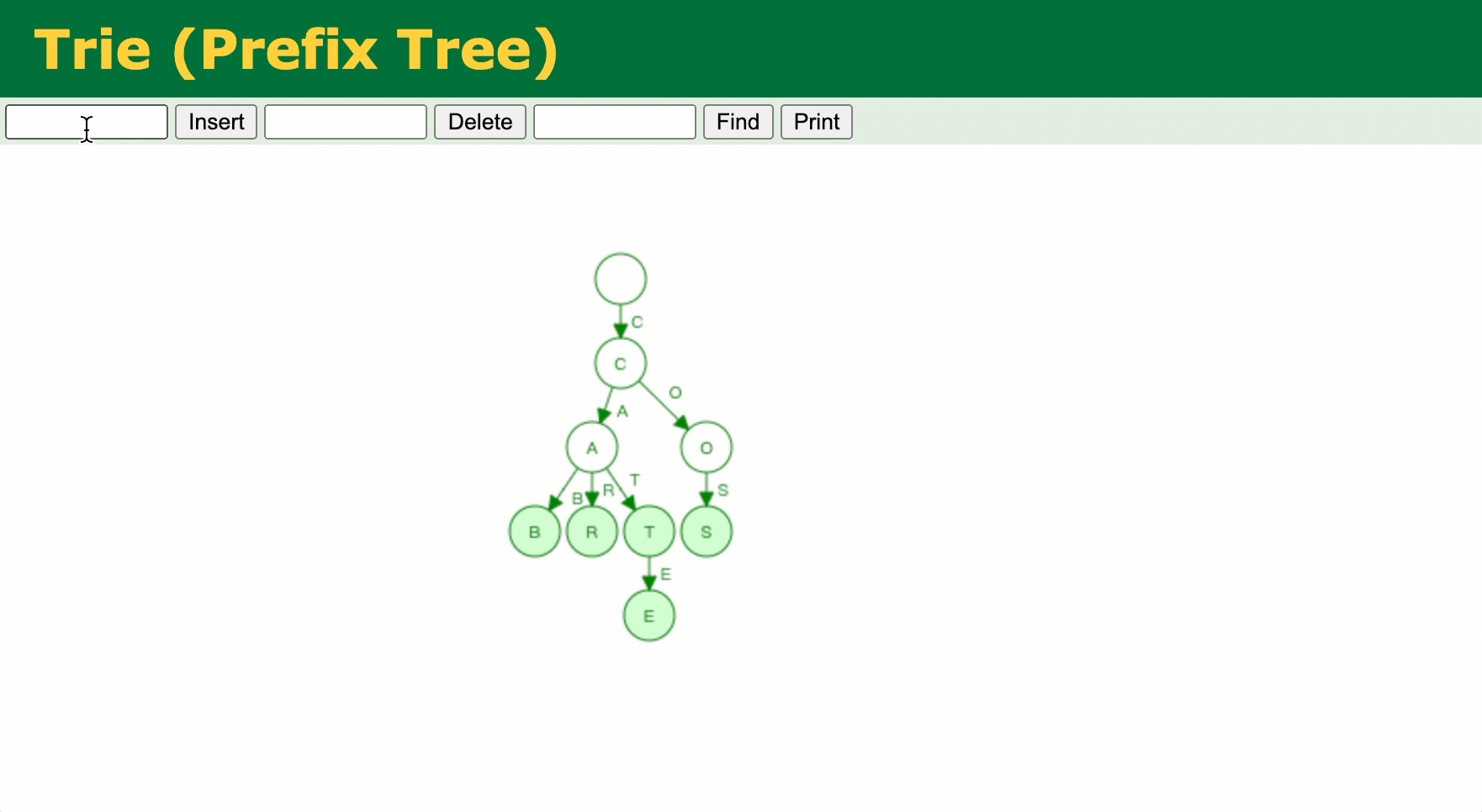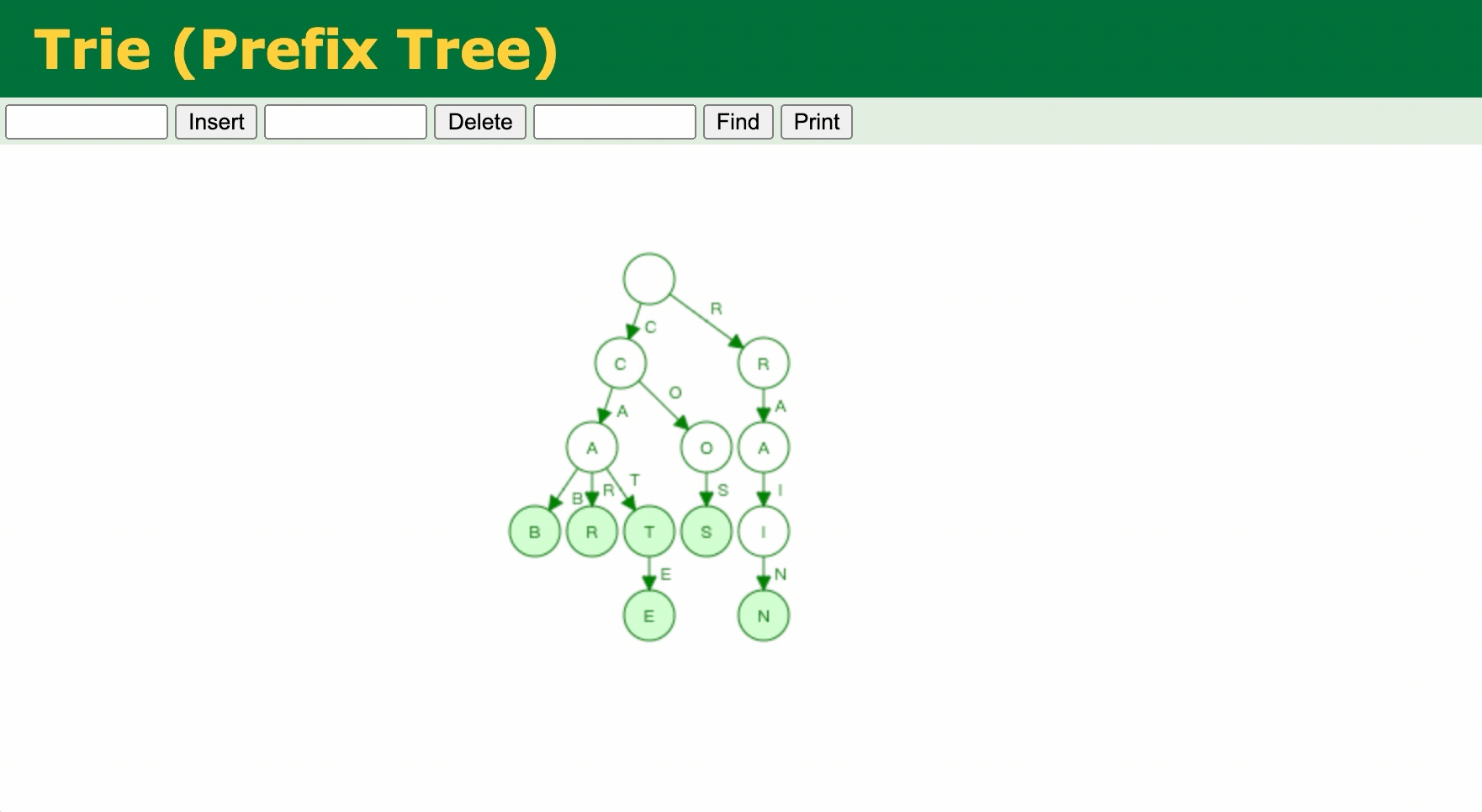
下面是建树、查找的代码实现
// tr[i][j] 表示下标 i 节点下 j 号子节点的下标, 此处26是仅有小写字母的合集
// idx 是自增的下标
int tr[M][26], idx;
// 插入某个字符串
void insert(char *str) {
// 初始化为根节点,表示当前节点
int p = 0;
for (int i = 0; str[i]; i++) {
int u = str[i] - 'a';
// 如果子节点不存在,创建一个新节点
if (!tr[p][u]) tr[p][u] = ++idx;
// 更新往下迭代
p = tr[p][u];
}
}
// 查询某个字符串的信息,这里可以统计单词个数、前缀个数等
int query(char *str) {
int p = 0;
for (int i = 0; str[i]; i++) {
int u = str[i] - 'a';
// ...
p = tr[p][u];
}
// 根据题目返回一些信息
return sth;
}
2. Trie 的一些基本使用
2.1 【例题】字符串统计
维护一个字符串集合,支持两种操作:
I x向集合中插入一个字符串 x;Q x询问一个字符串在集合中出现了多少次。共有 N 个操作,输入的字符串总长度不超过 ,字符串仅包含小写英文字母。
输入格式
第一行包含整数 N,表示操作数。
接下来 N 行,每行包含一个操作指令,指令为
I x或Q x中的一种。输出格式
对于每个询问指令
Q x,都要输出一个整数作为结果,表示 x 在集合中出现的次数。每个结果占一行。
数据范围
输入样例:
5 I abc Q abc Q ab I ab Q ab输出样例:
1 0 1
实现代码如下
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10;
int tr[N][26], idx, cnt[N];
char op[2], str[N];
void insert(char *str) {
int p = 0;
for (int i = 0; str[i]; i++) {
int u = str[i] - 'a';
if (!tr[p][u]) tr[p][u] = ++idx;
p = tr[p][u];
}
cnt[p]++;
}
int query(char *str) {
int p = 0;
for (int i = 0; str[i]; i++) {
int u = str[i] - 'a';
if (!tr[p][u]) return 0;
p = tr[p][u];
}
return cnt[p];
}
int main() {
int n;
cin >> n;
for (int i = 0; i < n; i++) {
scanf("%s%s", op, str);
if (op[0] == 'I') insert(str);
else cout << query(str) << endl;
}
return 0;
}
2.2 【例题】最大异或对
在给定的 N 个整数 $A_1,A_2……A_N $中选出两个进行 xor(异或)运算,得到的结果最大是多少?
输入格式
第一行输入一个整数 N。
第二行输入 N 个整数 。
输出格式
输出一个整数表示答案。
数据范围
输入样例:
3 1 2 3输出样例:
3
实现代码如下
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10, M = 31 * N;
int tr[M][2], idx, nums[N];
void insert(int x) {
int p = 0;
for (int i = 30; i >= 0; i--) {
int u = x >> i & 1;
if (!tr[p][u]) tr[p][u] = ++idx;
p = tr[p][u];
}
}
int query(int x) {
int p = 0, ret = 0;
for (int i = 30; i >= 0; i--) {
int u = x >> i & 1;
if (tr[p][u ^ 1]) p = tr[p][u ^ 1], ret += (1 << i);
else p = tr[p][u];
}
return ret;
}
int main() {
int n, x;
cin >> n;
int tot = -1;
while (n--) {
cin >> x;
insert(x);
nums[++tot] = x;
}
int ans = 0;
for (int i = 0; i <= tot; i++) {
ans = max(ans, query(nums[i]));
}
cout << ans << endl;
return 0;
}
3. https://leetcode-cn.com/problems/maximum-genetic-difference-query/
离线dfs + trie
const int N = 1e5 + 100;
const int B = 18;
typedef pair<int, int> PII;
class Solution {
int idx = 1;
int node[N*B][2];
int cnt[N*B];
unordered_map<int, vector<PII>> qm;
unordered_map<int, vector<int>> sm;
int head;
void insert(int v) {
int cur = head;
cnt[cur]++;
for(int i=B-1;i>=0;i--) {
int t = v >> i & 1;
if(node[cur][t] == 0) {
node[cur][t] = idx++;
}
cur = node[cur][t];
cnt[cur]++;
}
}
void erase(int v) {
int cur = head;
cnt[cur]--;
for(int i=B-1;i>=0;i--) {
int t = v >> i & 1;
if(cnt[node[cur][t]] == 1) {
node[cur][t] = 0;
return;
}
cur = node[cur][t];
cnt[cur]--;
}
}
int findMax(int v) {
int ret = 0;
int cur = head;
for(int i=B-1;i>=0;i--) {
int t = v >> i & 1;
if(node[cur][t^1] > 0) {
cur = node[cur][t^1];
ret += 1 << i;
} else {
cur = node[cur][t];
}
}
return ret;
}
vector<int> ans;
void dfs(int u) {
insert(u);
vector<PII>& p = qm[u];
for(int i=0;i<p.size();i++) {
PII& t = p[i];
int tmp = findMax(t.first);
ans[t.second] = findMax(t.first);
}
vector<int>& son = sm[u];
for(int s : son) {
dfs(s);
}
erase(u);
}
public:
vector<int> maxGeneticDifference(vector<int>& ps, vector<vector<int>>& qs) {
head = idx++;
int qsize = qs.size();
for(int i=0;i<qsize;i++) {
auto& q = qs[i];
qm[q[0]].push_back({q[1], i});
}
for(int i=0;i<ps.size();i++) {
sm[ps[i]].push_back(i);
}
ans.resize(qs.size());
dfs(sm[-1][0]);
return ans;
}
};