1.线段树基本介绍与实现

树状数组是一种基于分治思想的二叉树结构，用于在区间上进行信息统计，与按照二进制位进行区间划分的树状数组相比，线段树更加通用：

1. 线段树每个节点都代表一个区间
2. 线段树具有唯一的根节点，代表的区间是整个统计范围，如 $[1, N]$
3. 线段树的每个叶子节点都代表一个长度为1的元区间 $[x, x]$
4. 对于每个内部节点 $[l, r]$，他的左子节点是 $[mid+1, r]$, 其中 mid = (l+r) >> 1

如下图所示，是一颗二叉树视角的线段树，我们要做的就是做好每个节点的统计信息。

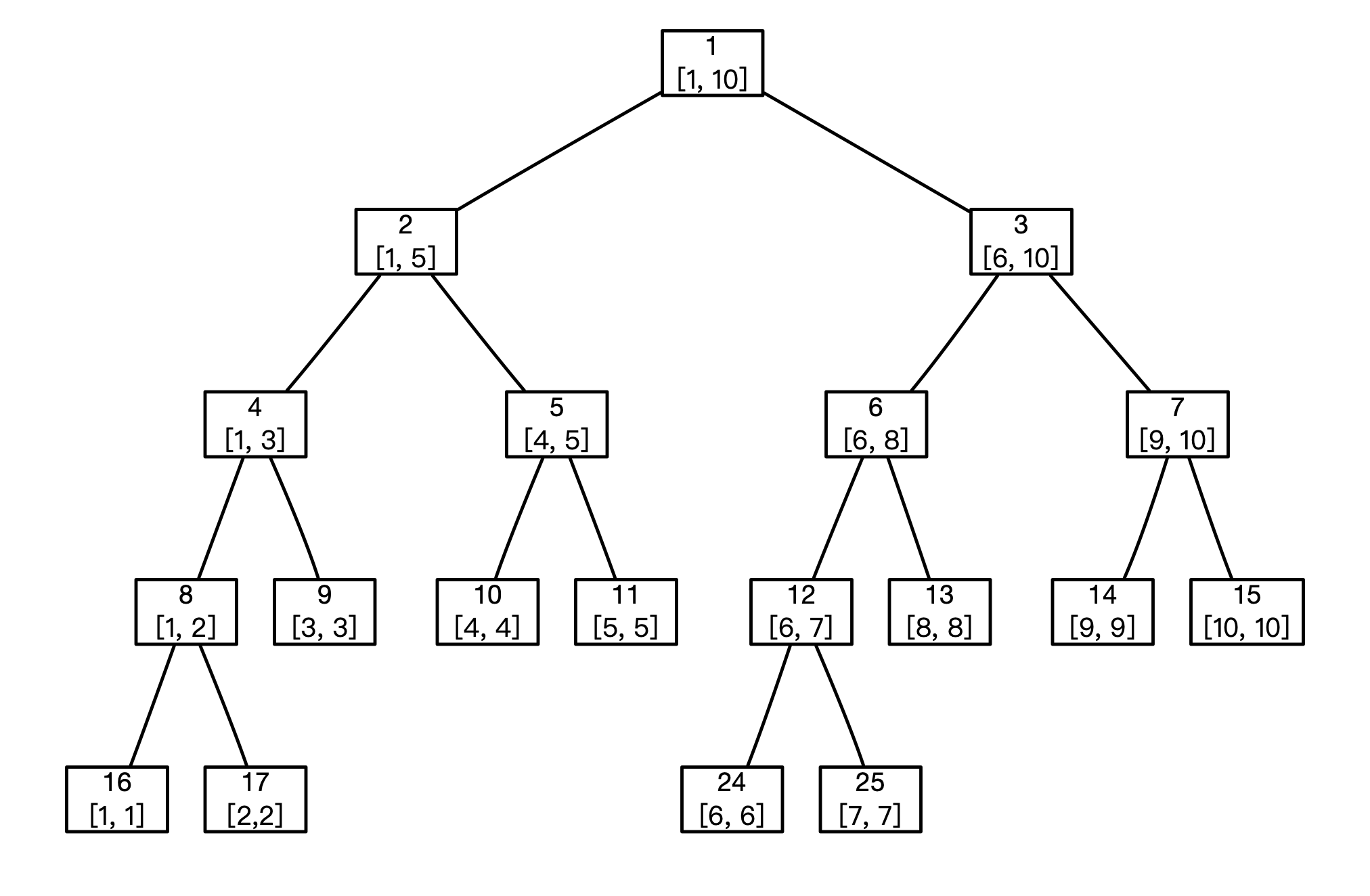
线段树查询、更新的时间复杂度是O(logN)，空间复杂度是O(4N)（至于为什么，可以参照上图证明下就可以了），支持区间操作的（区间操作的时候要做懒标记，即 pushdown 操作）。

下面是实现方式

struct Node
{
    int l, r;
    // TODO: 需要维护的信息和懒标记
}tr[N * 4];

void pushup(int u)
{
    // TODO: 利用左右儿子信息维护当前节点的信息
}

void pushdown(int u)
{
    // TODO: 将懒标记下传
}

void build(int u, int l, int r)
{
    if (l == r) tr[u] = {l, r};
    else
    {
        tr[u] = {l, r};
        int mid = l + r >> 1;
        build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
        pushup(u);
    }
}

void update(int u, int l, int r, int d)
{
    if (tr[u].l >= l && tr[u].r <= r)
    {
        // TODO: 修改区间
    }
    else
    {
        pushdown(u);
        int mid = tr[u].l + tr[u].r >> 1;
        if (l <= mid) update(u << 1, l, r, d);
        if (r > mid) update(u << 1 | 1, l, r, d);
        pushup(u);
    }
}

int query(int u, int l, int r)
{
    if (tr[u].l >= l && tr[u].r <= r)
    {
        return ;  // TODO 需要补充返回值
    }
    else
    {
        pushdown(u);
        int mid = tr[u].l + tr[u].r >> 1;
        int res = 0;
        if (l <= mid ) res = query(u << 1, l, r);
        if (r > mid) res += query(u << 1 | 1, l, r);
        return res;
    }
}

2. 一些基本使用

【例题1】最大数

给定一个正整数数列 $a_1,a_2,…,a_n$ 每一个数都在 0∼p−1 之间。

可以对这列数进行两种操作：

1. 添加操作：向序列后添加一个数，序列长度变成 n+1；
2. 询问操作：询问这个序列中最后 L 个数中最大的数是多少。

程序运行的最开始，整数序列为空。

一共要对整数序列进行 m 次操作。

写一个程序，读入操作的序列，并输出询问操作的答案。

输入格式

第一行有两个正整数 m,p，意义如题目描述；

接下来 m 行，每一行表示一个操作。

如果该行的内容是 Q L，则表示这个操作是询问序列中最后 LL 个数的最大数是多少；

如果是 A t，则表示向序列后面加一个数，加入的数是 (t+a) mod p。其中，t 是输入的参数，a 是在这个添加操作之前最后一个询问操作的答案（如果之前没有询问操作，则 a=0）。

第一个操作一定是添加操作。对于询问操作，L>0 且不超过当前序列的长度。

输出格式

对于每一个询问操作，输出一行。该行只有一个数，即序列中最后 LL 个数的最大数。

数据范围

$1≤m≤2×10^5$
$1≤p≤2×10^9$
$0≤t<p$

输入样例：

10 100
A 97
Q 1
Q 1
A 17
Q 2
A 63
Q 1
Q 1
Q 3
A 99

输出样例：

97
97
97
60
60
97

样例解释

最后的序列是 97,14,60,96

实现代码如下

#include <iostream>
#include <cmath>
#include <algorithm>
#include <vector>

using namespace std;

const int N = 2e5 + 10;

struct Node {
    int l, r;
    int val;
} tr[N << 2];

void pushUp(int u) {
    tr[u].val = max(tr[u << 1].val, tr[u << 1 | 1].val);
}

void build(int l, int r, int u) {
    tr[u].l = l, tr[u].r = r;
    if (l == r) return;
    int mid = l + r >> 1;
    build(l, mid, u << 1);
    build(mid + 1, r, u << 1 | 1);
}

void modify(int u, int i, int v) {
    int l = tr[u].l, r = tr[u].r;
    if (l == r) {
        tr[u].val = v;
        return;
    }
    int mid = l + r >> 1;
    if (i <= mid) modify(u << 1, i, v);
    else modify(u << 1 | 1, i, v);
    pushUp(u);
}

int query(int l, int r, int u) {
    if (tr[u].l >= l && tr[u].r <= r) return tr[u].val;
    int mid = tr[u].l + tr[u].r >> 1;
    if (r <= mid) return query(l, r, u << 1);
    else if (l > mid) return query(l, r, u << 1 | 1);
    else return max(query(l, mid, u << 1), query(mid + 1, r, u << 1 | 1));
}

int main() {
    int m, p, k, n = 0;
    int last = 0;
    build(1, N, 1);
    cin >> m >> p;
    while (m--) {
        char op[2];
        scanf("%s%d", op, &k);
        if (op[0] == 'Q') {
            last = query(n - k + 1, n, 1);
            cout << last << endl;
        } else {
            modify(1, ++n, (k + last) % p);
        }
    }
    return 0;
}